Quantum Computing for Classical Developers

A disclaimer before I even get started: I’m not a physicist, haven’t studied quantum mechanics or quantum computing in any way. During the day, I’m actually a “normal” web developer.

This is just something I’m passionate about; most of it is self-taught through online courses, tutorials and other materials I could find access to. So please see the talk through this lens: an exploration of how quantum computing works and how it might be applied in the future from the perspective of a “classical” software engineer.

Also, slightly controversial, I usually like to start these kinds of talks with the key takeaways in the beginning. Just because I feel it often helps to give some guidance, especially around topics that otherwise could be hard to follow.

So this is the core key takeaway of this talk: quantum computers won’t replace classical computers.

Instead, it’s much more accurate to think of them as enhancements for classical computers, doing a special range of computation.

On top of that, I also think the word “quantum computer” is pretty misleading in that sense. So in my talk, I’ll either refer to it more broadly as quantum computing or, even better, as a quantum processing unit, which is also what manufacturers call them.

It encourages the mental image that, similar to e.g. a GPU, a QPU sits on top of the normal computer and is utilised only for those specific kinds of computations the unit is good at.

Like with GPUs, it’s also much more important to understand how it works conceptually and what that special kind of computation is, at least in my opinion. You don't need to know how to build a GPU to be able to write code for it, same goes with QPUs, at least in my opinion. So this won’t be a 60min deep dive into quantum mechanics; sorry if you were expecting that. Instead, I’m hoping I’ll be able to explain the difference between classical and quantum computing, give some practical examples of the kinds of problems QPUs have the potential to solve.

Alright, enough introduction, let’s dive into it: what are the fundamental differences between classical and quantum computing. Probably the main and most important difference is how information is stored.

In classical computing, we have "classical" bits, and in quantum computing we have, well, "quantum" bits, or qubits.

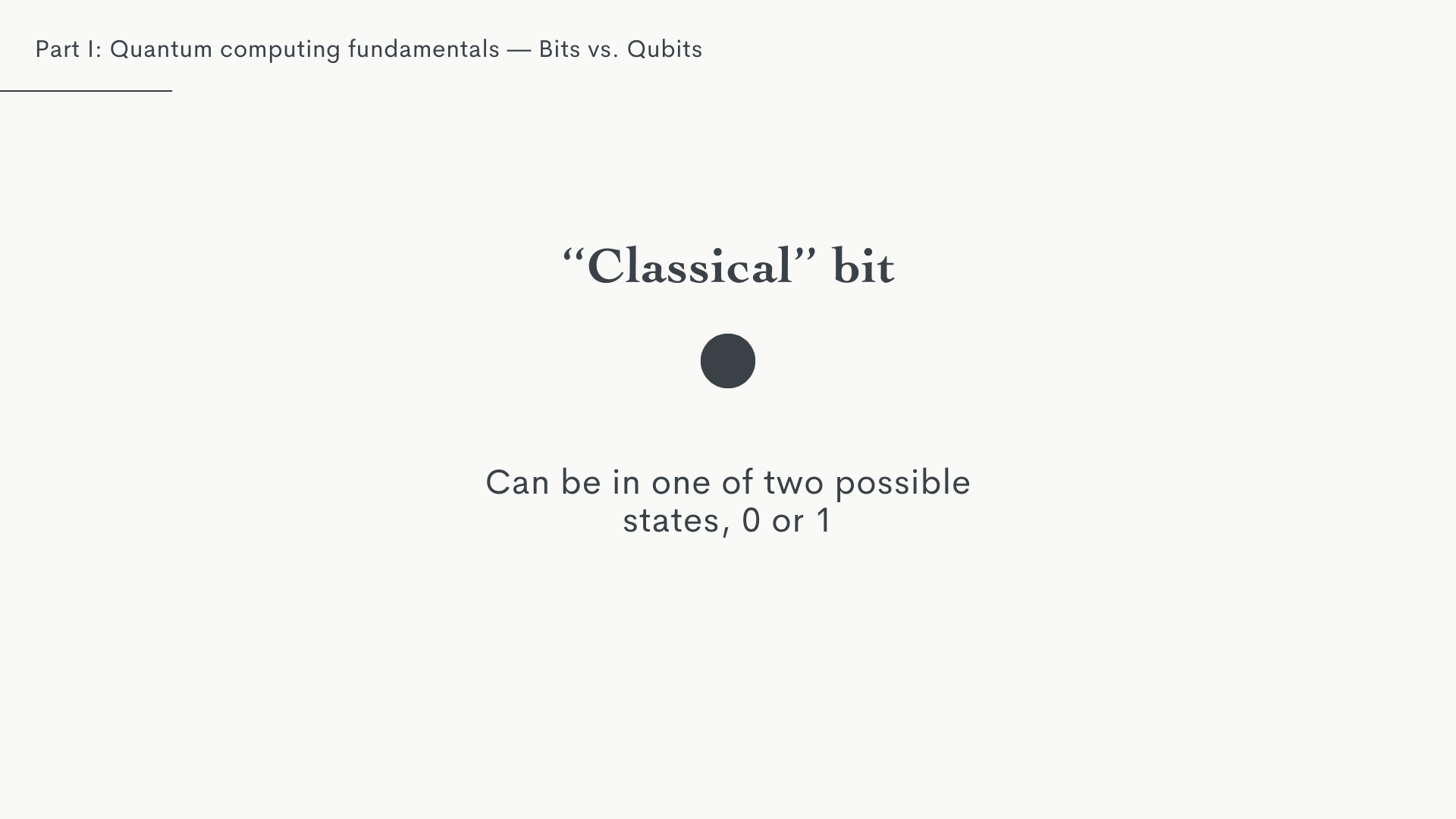
Classical bits we’re hopefully all pretty familiar with; they can store a value of 0 or 1.

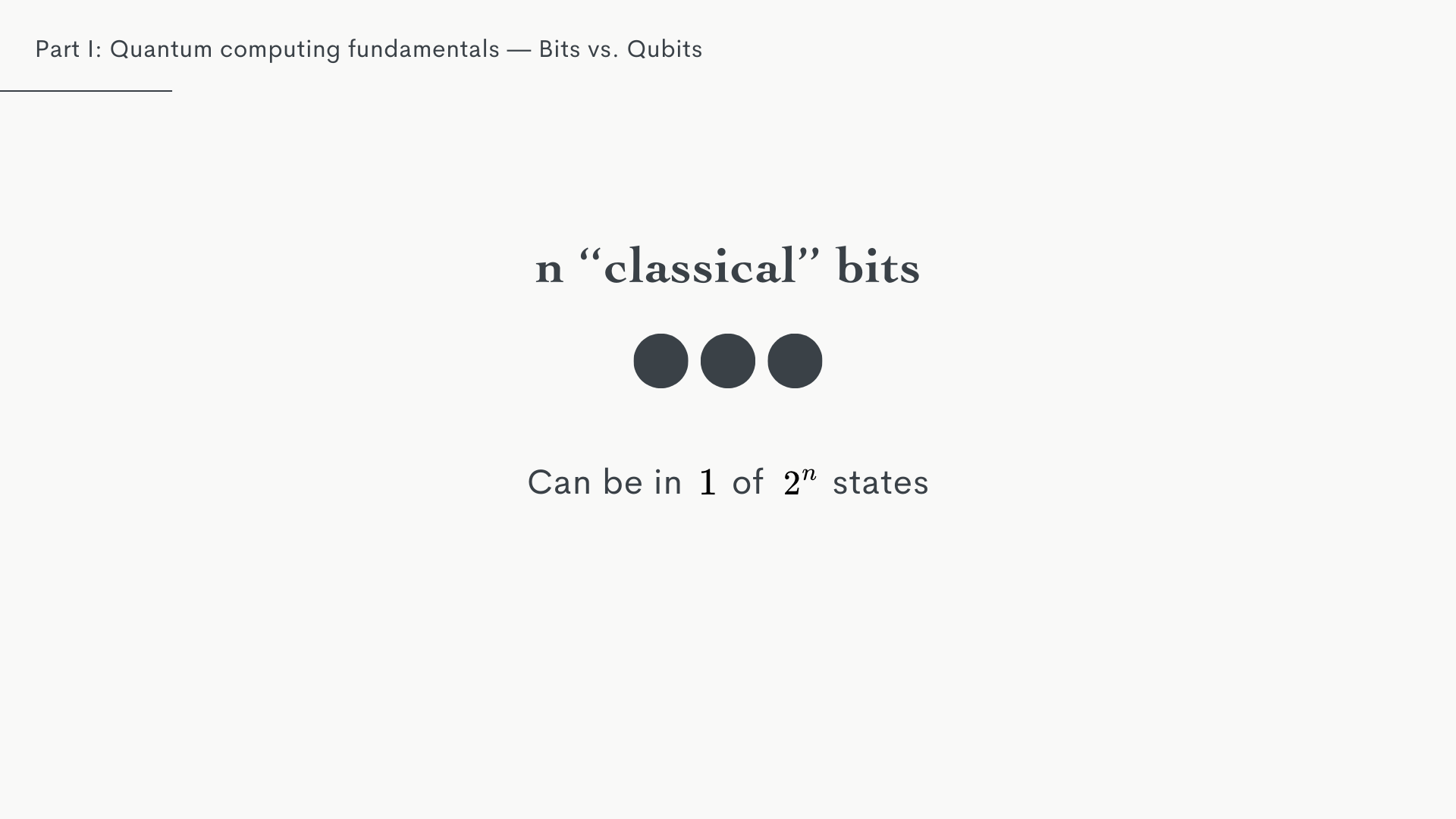
When we have multiple bits, we can combine them to represent 1 of $2^n$ states. And we can use logic gates like AND, OR and NOT to represent any kind of algebraic calculation.

This is what made digital computers so successful, the fact that fundamentally they are quite simple, but through these simple building blocks we were able to express all the complex problems we wanted to solve.

Qubits can also be in two states, 0 and 1. But unlike classical bits, they take advantage of something called “superposition”. It allows them to be in both states at the same time.

Which we can write like this; I'm simplifying a bit here, ignoring some of the fluff we don't need for the purpose of this talk.

This means instead of 1 of $2^n$ states, qubits can represent all $2^n$ states simultaneously: $|0\rangle + |1\rangle$

There’s a famous experiment which I think is a great visual explanation for the effects of superposition: the double-split experiment. You might have covered this in school, but here's a quick refresher.

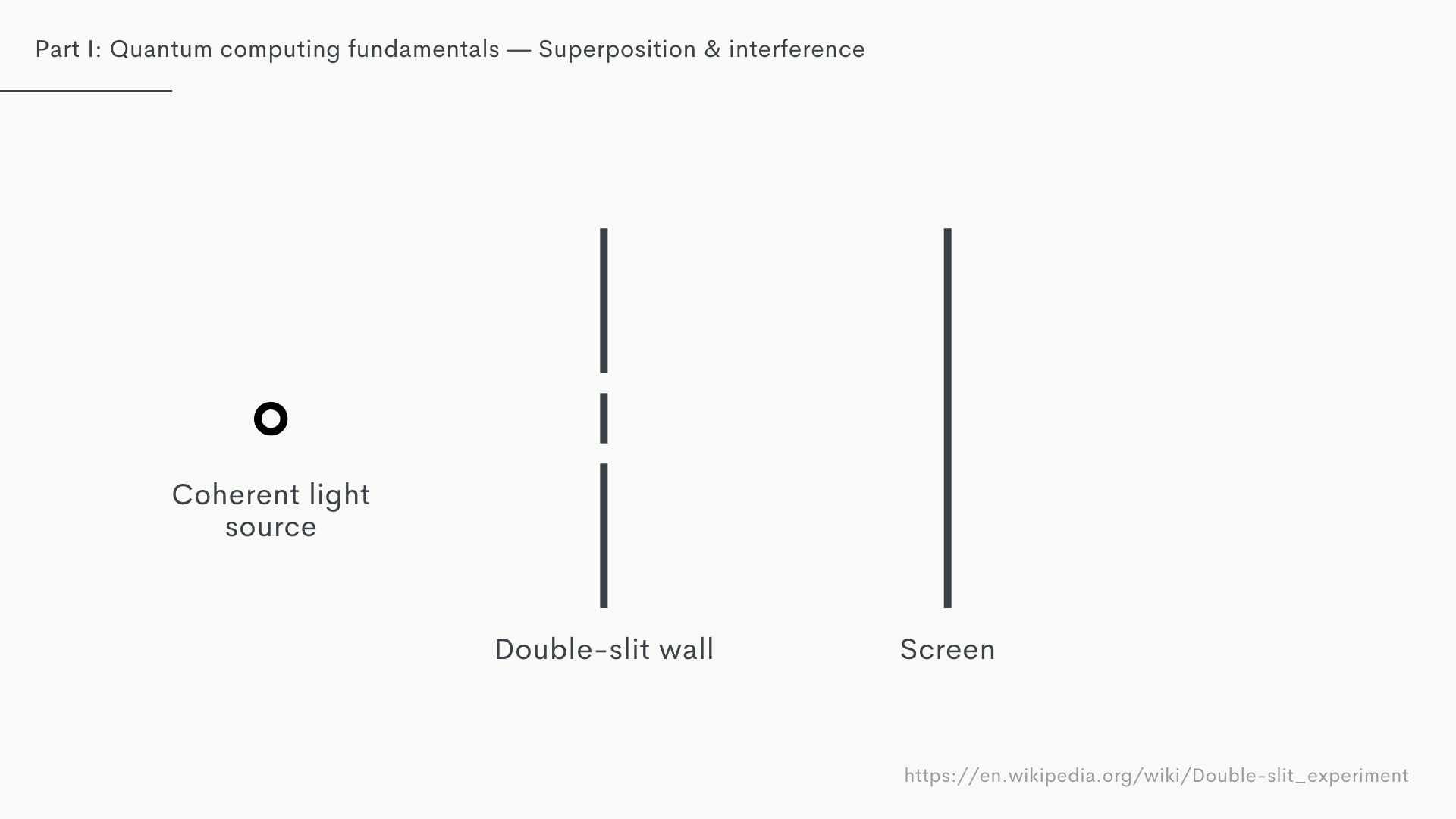
In the double split experiment, we shoot a light, usually a laser, through two tiny gaps in a wall against a screen in the background.

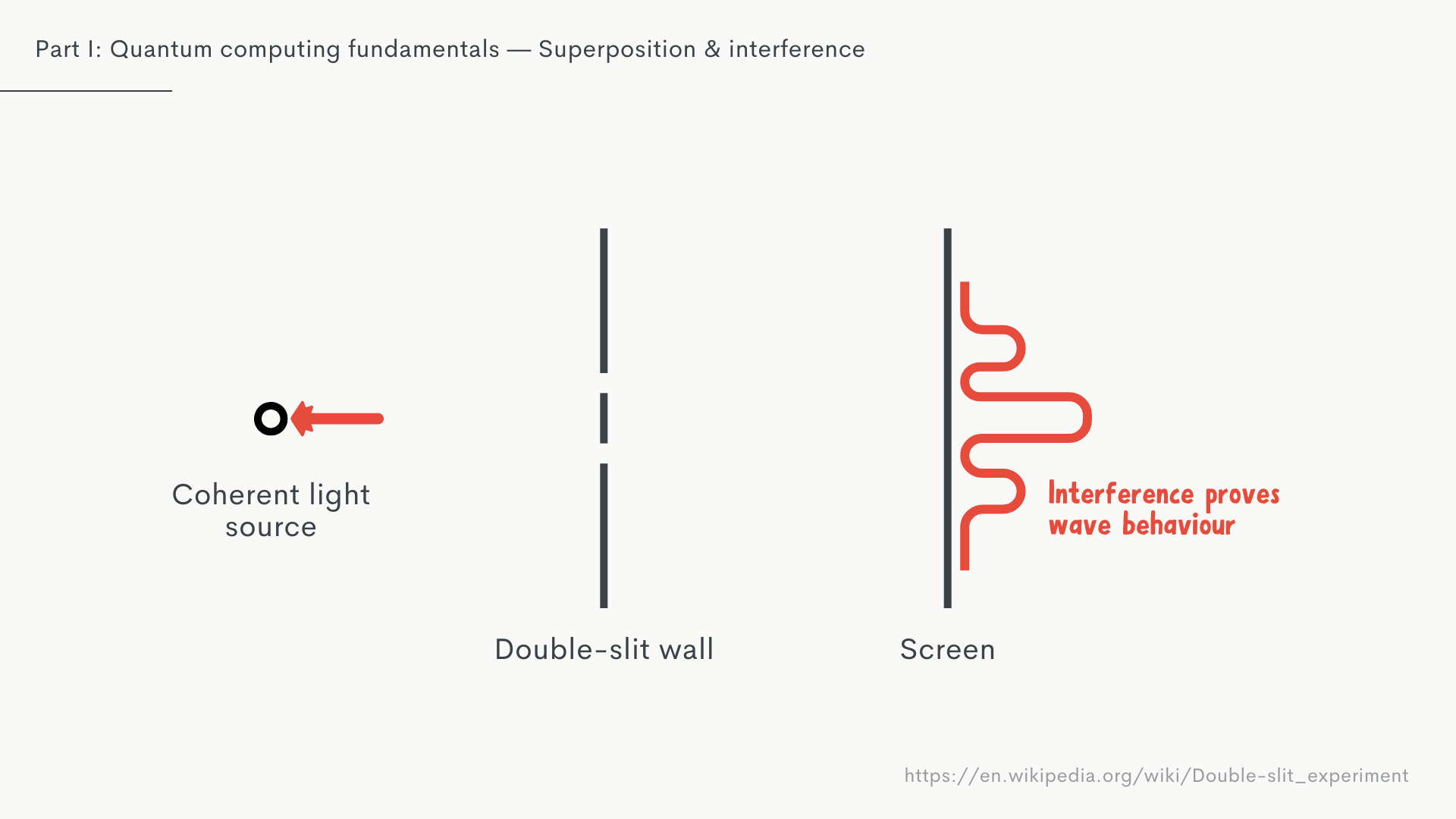
When we turn the laser on, the light creates an interference pattern. This proves that light behaves like waves, interfering with itself when going through the slits.

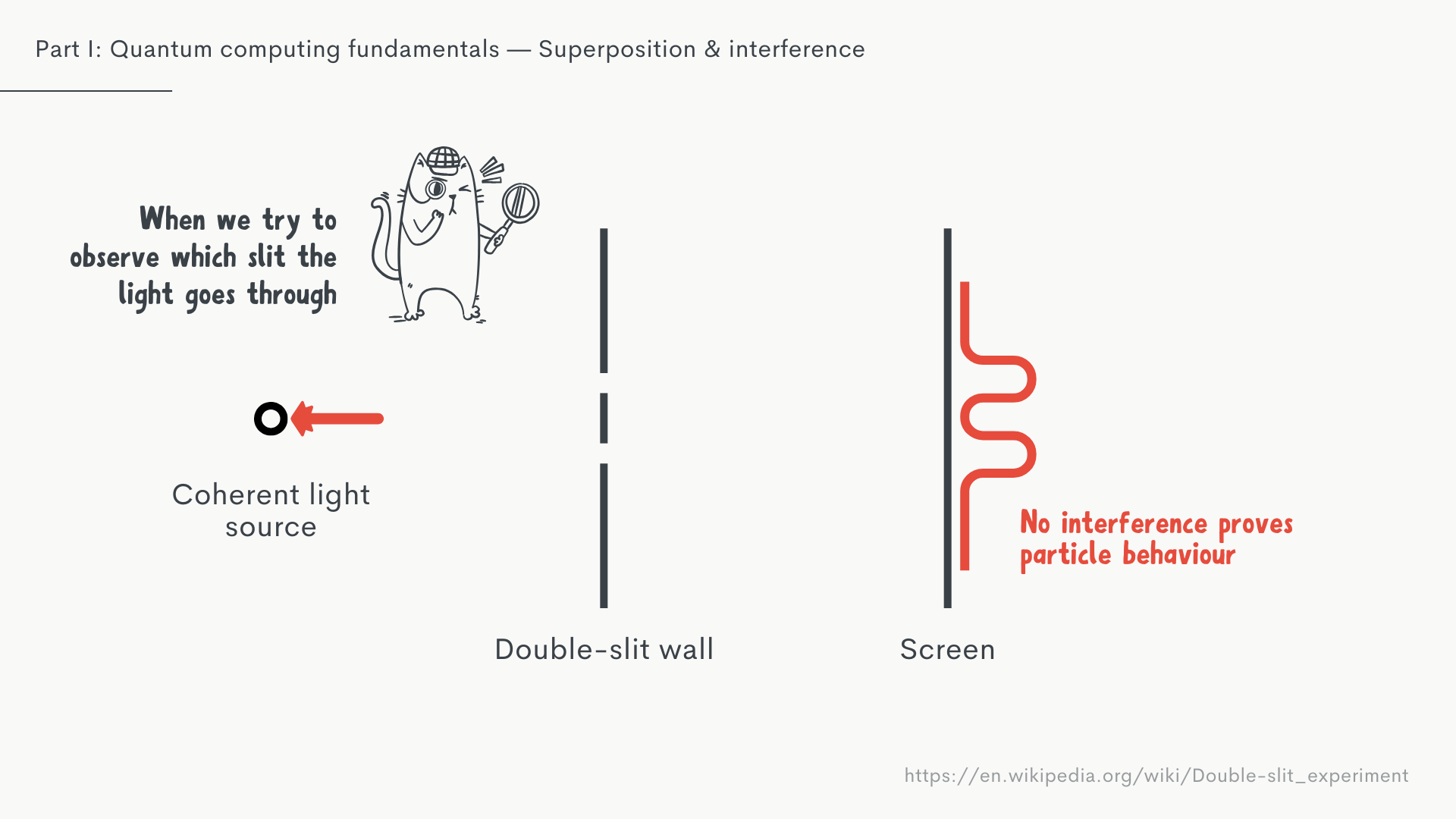
However, the moment we try to observe which slit the light goes through, that interference pattern disappears. We end up with a pattern that reflects how light would behave if it were particles, like tiny little billiard balls. This is what we call particle-wave-duality.

Photons and other fundamental particles can have the attributes of both particles and waves, and it changes when it’s being observed, or more accurately: “measured”.

The important thing here, that I, for example, haven’t been taught in high school (or I just wasn’t really paying attention), is that this phenomenon also occurs when the photons are sent through the double split one at a time. Meaning, without being measured, the photons interfere with themselves; they represent a wave that describes the distribution of all the possible ways it could go. And once they are measured, their “wave properties” collapse and they behave like particles, with just one possible way they can go: the one we measured.

I’ll leave it here, but if you want your mind blown a bit more, look up the delayed choice quantum eraser variation of this experiment.

To bring this back to our qubits, similar to the photons in the double split experiment, they can be thought of as a wave function describing the probabilities of all possible states at the same time.

So in quantum computing, if we have a problem, say: we want to find what plus 2 equals 3. We can pass in a superposition of all possible answers for $x$, and we will get as a result a superposition of all inputs and $true$ or $false$, based on the calculation we are doing.

But similar to the double-slit experiment, we can't actually measure this superposition.

The moment we try, the superposition will simply collapse and based on its probabilities return a random single answer, e.g. that the input 2 leads to the result $false$. Which is not very helpful, and hopefully shows that we can't use quantum computing to brute force our way through problems, it's a bit more complicated than that.

The real power of quantum computing, or more specially quantum algorithms, lies in the interference piece. Essentially, the goal of quantum algorithms is to make the states in your superposition interfere in a way that all wrong answers destructively interfere, and all right answers constructively interfere. That means, when you measure the result and the superposition collapses, you will get the right answer.

Now this might be pretty confusing right now, we'll take a look at a practical example what this actually means in a second. For now the important part to understand is that superposition doesn't allow us to just throw more inputs at classical computation problems to get results faster, that's not how it works.

There is one more quantum phenomenon that somewhat ties into all of this, which is the concept of entanglement.

I won’t go too much into detail here because of time constraints, but in a nutshell, it describes a process where you can “connect” two qubits with each other in a way that their state, even though it’s in a superposition and not deterministic until measured, becomes dependent on each other. Then, when you measure one, you also know the value of the other.

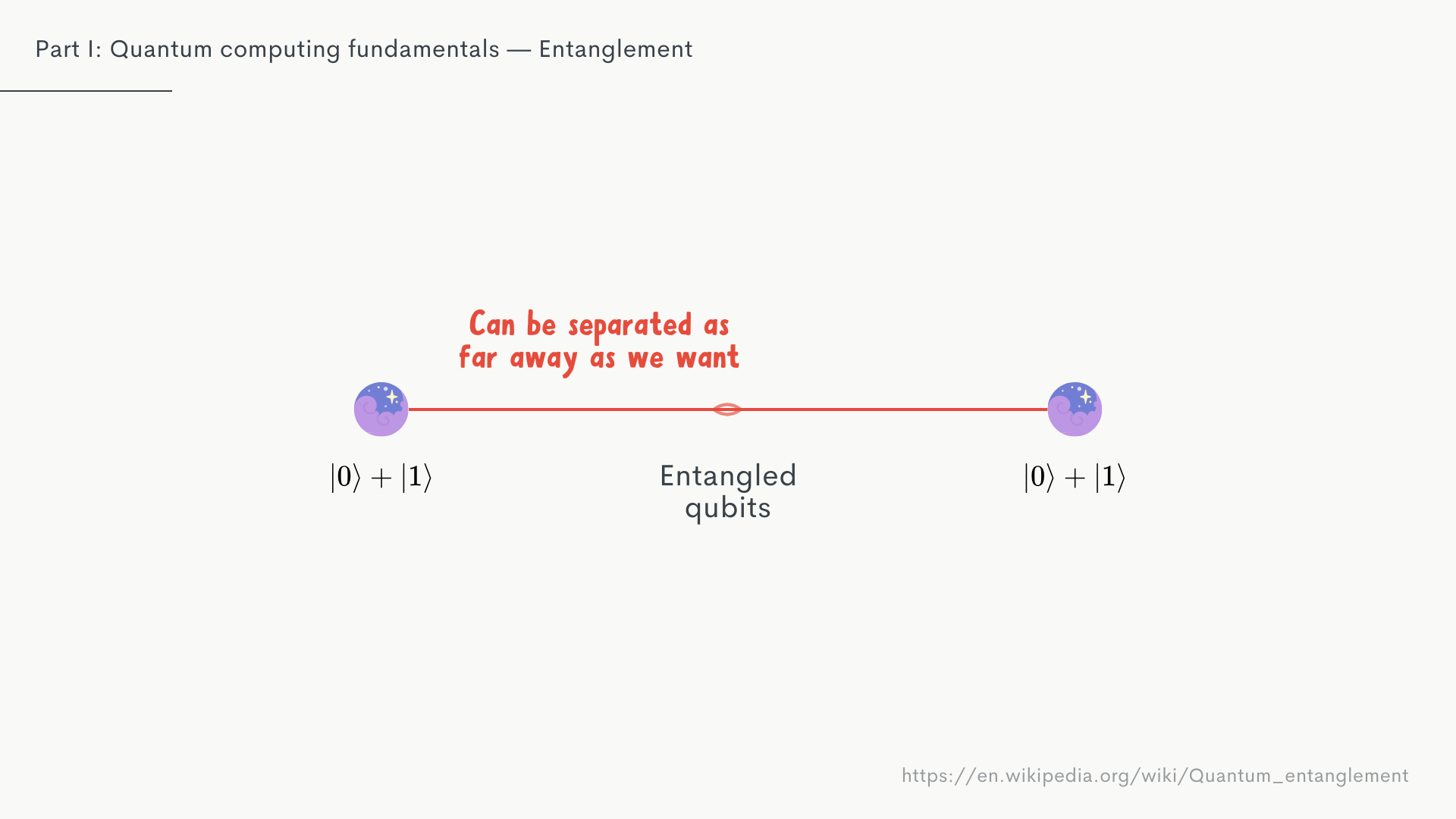
The interesting, and arguably freaky, thing here is that it doesn't matter how far of a distance you create between these two qubits after you've entangled them.

Once you measure one, both their states collapse. The relevance here is that this allows us to manipulate our quantum state in specific ways, e.g. to get it into those setups that allow us to take advantage of interference.

But it’s also just an interesting concept in itself. Einstein famously described as “spooky action at a distance” - which he probably didn’t really say cause it’s on the internet and the internet always lies, but still 😄

It’s also the cause for a lot of controversies, fuelled mainly by misinterpretations, that this would allow for faster-than-light communication since entangled particles can be separated by any distance you want, and the measurement is instant. It obviously doesn’t, and there's a lot of good research and explanaitions out there on the internet to show why, but it’s nonetheless an interesting Youtube rabbit hole to get into if you have a weekend to spare.

Ok, let’s try to put all of this theory into a practical example. One of the most famous, if not the most famous, practical applications of quantum computing is Shor’s algorithm, which promises to break modern encryption as we know it.

When I say modern encryption, I mostly mean RSA encryption. It's the go to standard on the web these days, we're using it e.g. for things like SSH. And it takes advantage of one simple mathematical fact: with classical methods, for a known large number, it’s really really hard to find its factors.

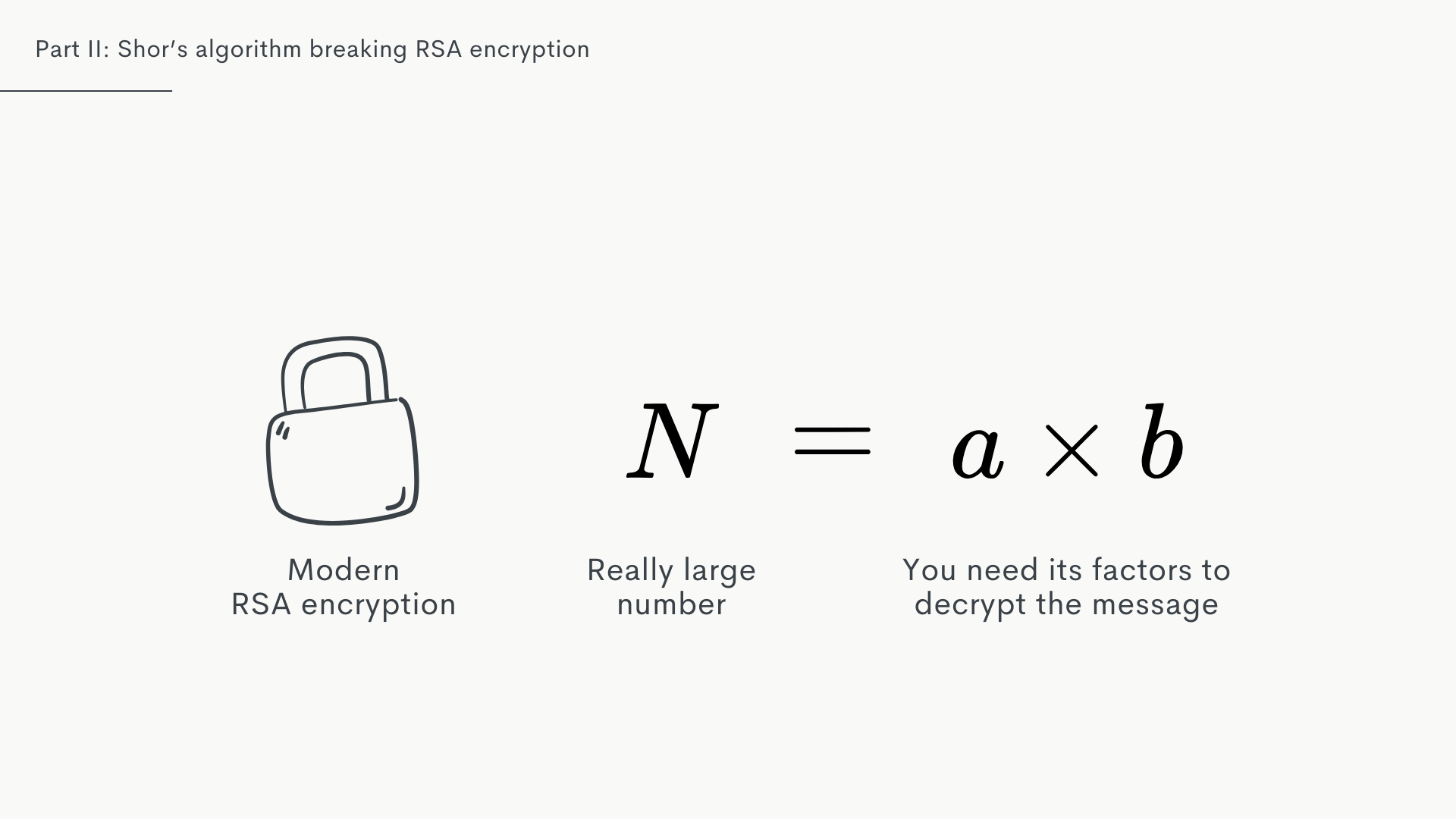
For RSA, you need these factors of an extremely large number to decrypt the message.

It's easy to take two numbers and multiply the together. But if you just have a large number, it's hard to do it in reverse and takes a really long time.

Exponentially long, in fact, based on the number of digits of your large number.

Using a number with 50 digits e.g., a normal computer would take around 10 minutes to find the factors and break it. A 60 digit number would already take ~2hrs. A 70 digit number ~20hrs.

The rule of thumb here being every 10 digits increase the time it takes to compute by a multiple of 10. So once we get to RSA-2048, which is the current recommended standard e.g. used for things like SSH, we get to a processing time of $\approx 2.28 * 10^{1984} \text{ years}$, which is unfathomably large.

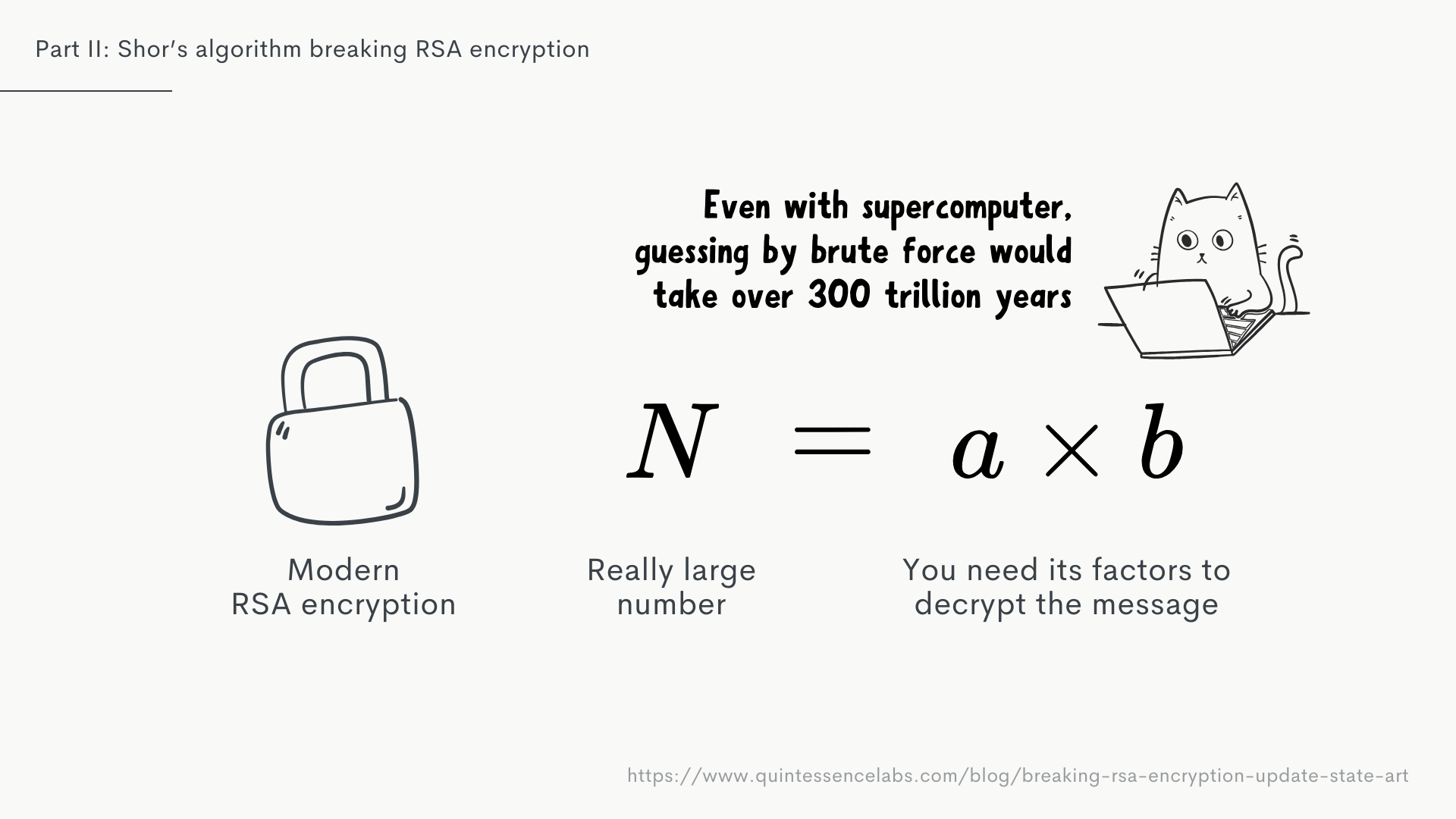
Even on the fastest supercomputers we have today, it would take over 300 trillion years to factor a 2048 bit number.

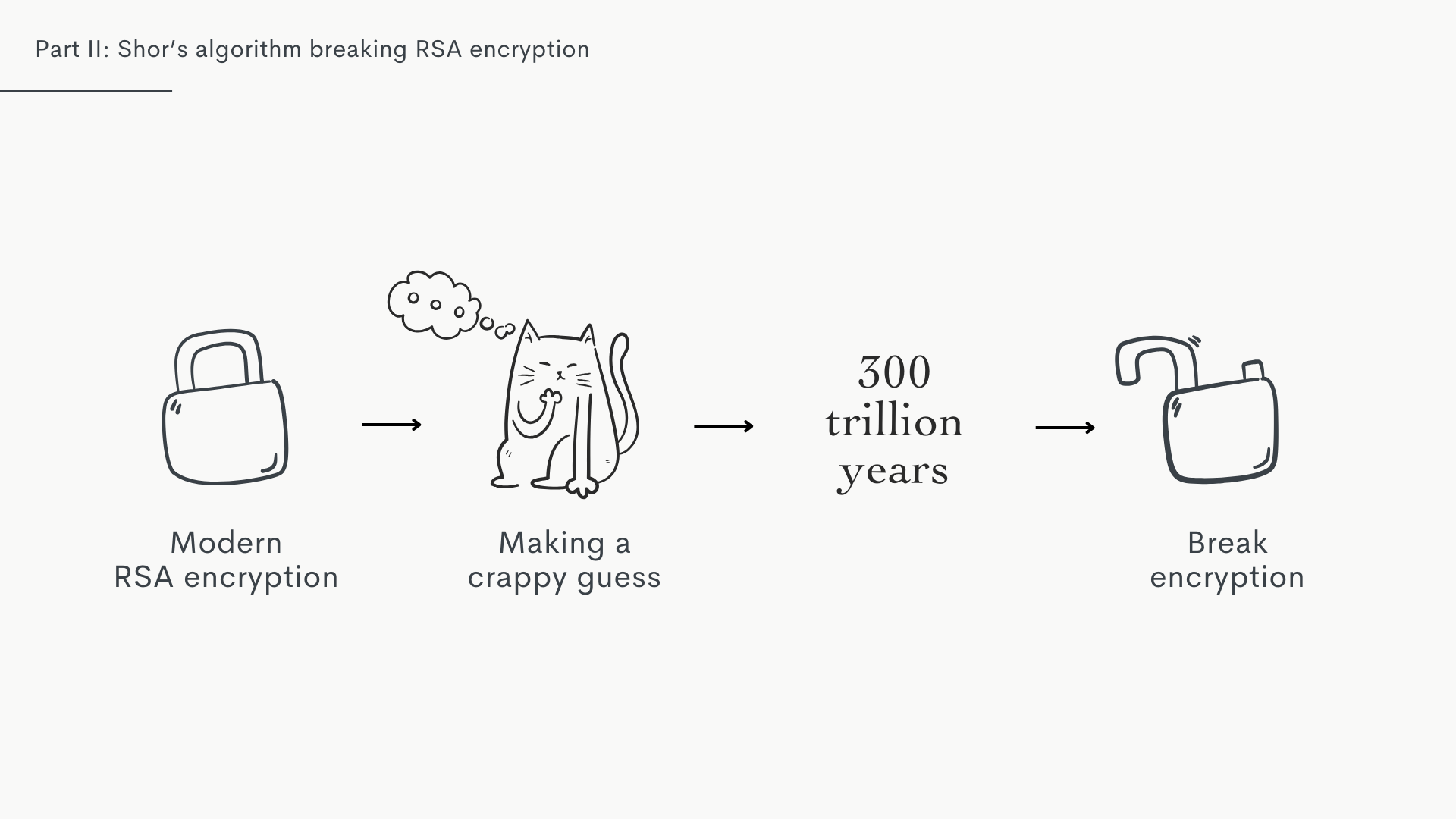
Which is why we consider it a safe method, because even though it's technically possible to break it, it takes so long that it's impractical.

But what if we had a magical box, that takes our bad guess for the factors and turns it into a good guess?

That magical box is essentially what Shor’s algorithm is. And it starts with another mathematical fact.

If you take two numbers that don’t share factors, when you multiply one of them enough times with itself, it will eventually result in a multiple of the other number plus one.

Using more appropriate variable names, we have $g$ for our guess and $N$ for the large number we want to find the factors for.

By definition, if we made a bad guess, they don't share factors with each other. If they share factors, there's a very old but very efficient method called Euclid's algorithm that helps us find the shared factor and break the encryption.

So, since they don't share factors for a bad guess, the rule I just mentioned applies and we can write it as: $g^p = m * N + 1$

We can then re-arrange that equation: $(g^{p/2} + 1)*(g^{p/2} - 1) = m * N$

This is starting to look very familar, doesn't it? Something times something else equaling N. So with this fairly simple maths trick, we turned our bad guess $g$ into two much better guesses, $(g^{p/2} + 1)$ and $(g^{p/2} - 1)$

But there are a couple of potential problems with those better guesses.

For one, the new guess itself might be a multiple of $N$, which means the other would be a factor of $m$ and neither would be useful for us. But we can check for that very easily.

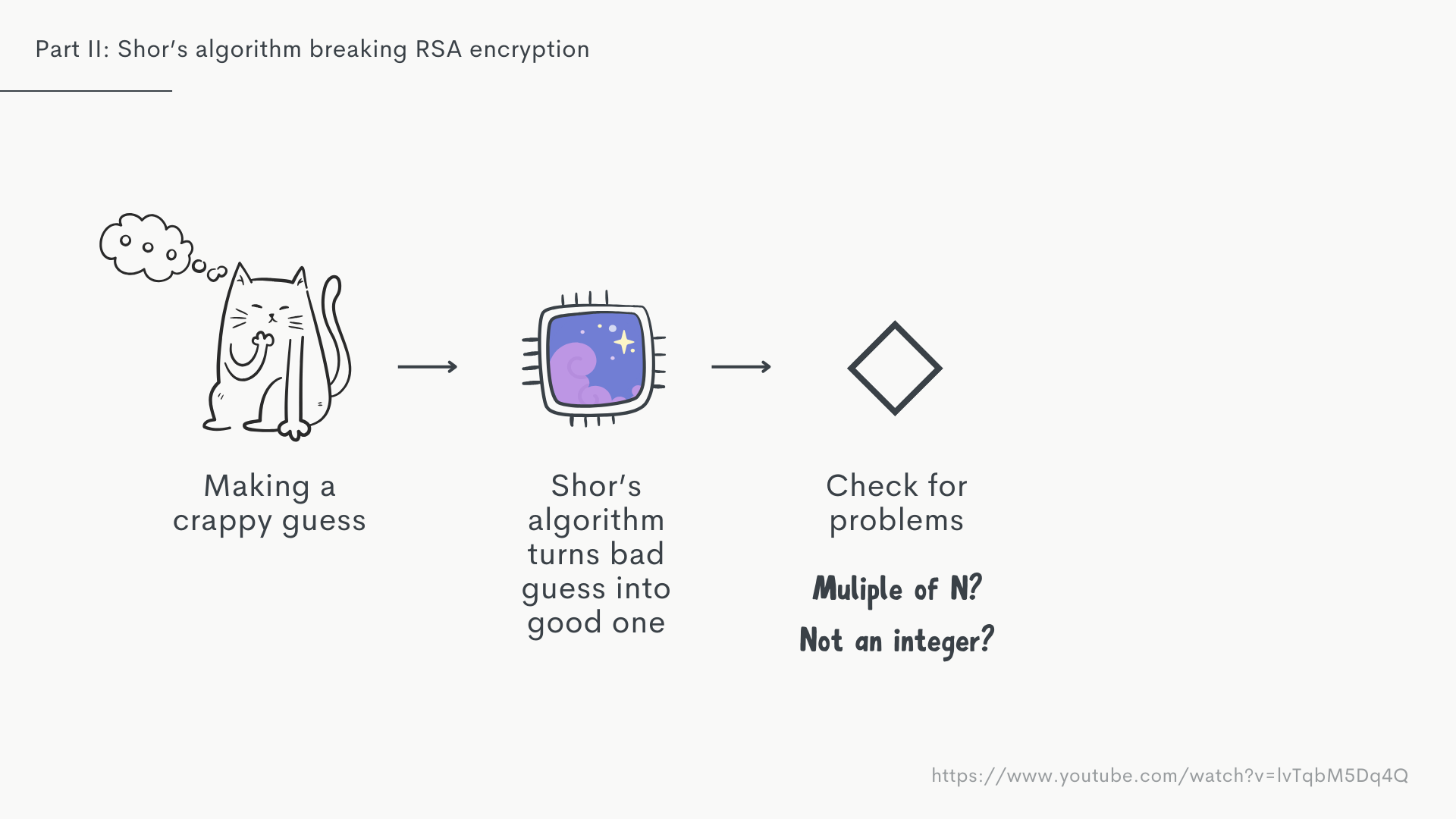
The other problem is that $p$ might not be a whole number, meaning our guess taken to the power of $p/2$ also won’t be, which is no good. We’re looking for integers.

But again, this is very easy to check for. And, more importantly, as it turns out, for any random guess $g$, neither of these two problems occur 37.5% of the time.

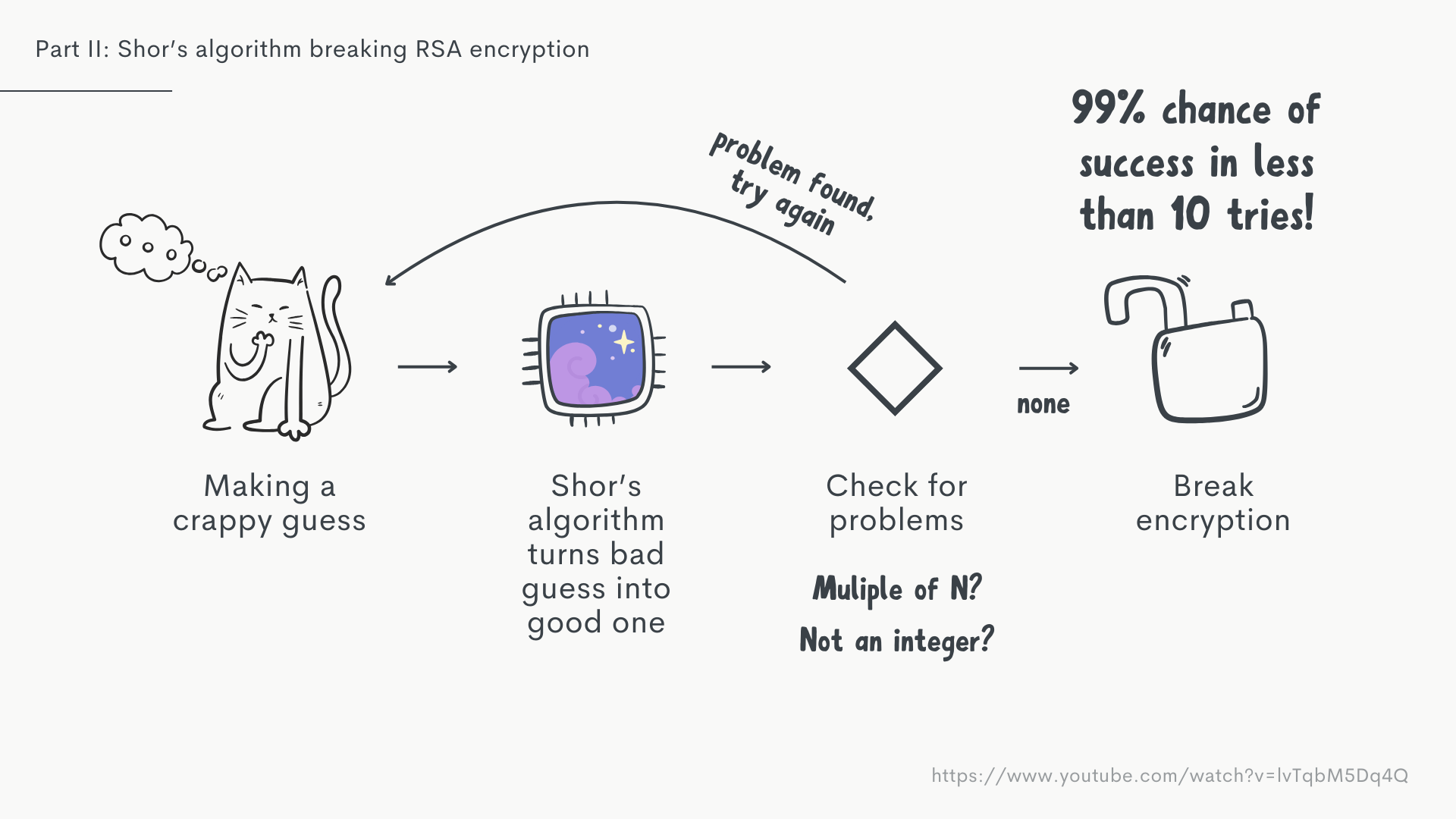
This is huge, it means that 99.9% of the time, we will be able to get a valid answer from a random crappy guess within 10 tries!

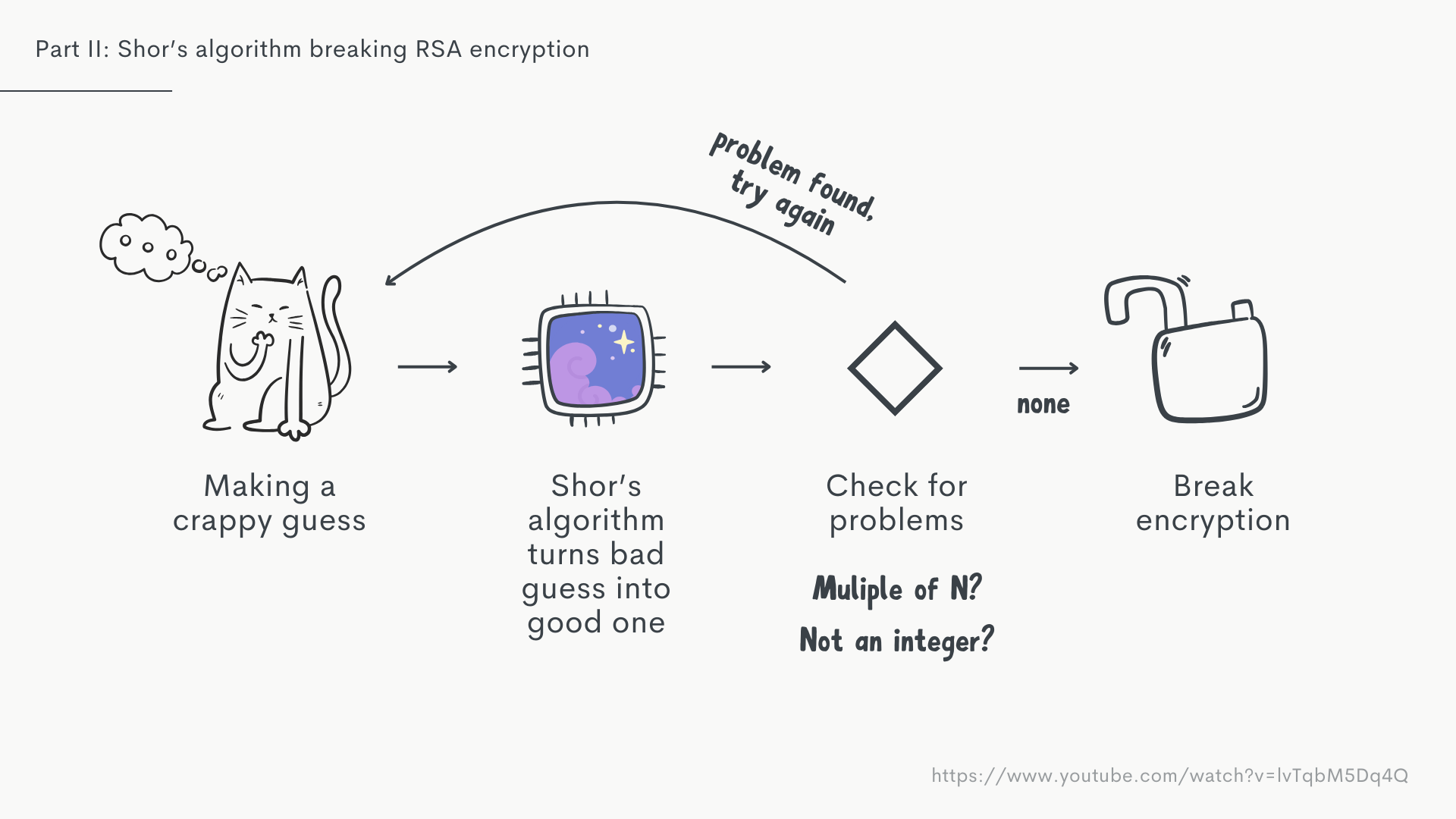
Ok, let's get to the elephant in the room.

Unsurprisingly finding that factor $p$ through classical methods is really really hard, we’re essentially back to brute force guessing and no better off than we were when we were originally just guessing the factors.

This is where finally the quantum computation part comes in, at least almost. There is another mathematical observation we can take advantage of.

If we take our original equation for the better guess: $g^p = m * N + 1$

We can re-write it as $g^p = 1 \mod N$. we don't really care about the $m$ part, what we do care about is the remainder, which is what the modulo expression focuses on.

Now, let’s just randomly pick a $p$, and measure the actual remainder we get. Very likely it's not 1 but something else, e.g.: $g^{42} = 3 \mod N$

Luckily for us, if we increase our guess for $p$ by the amount of the actual $p$, it turns out the remainder will stay the same. Meaning:

$g^{42} = 3 \mod N$
$g^{42 + p} = 3 \mod N$
$g^{42 + 2p} = 3 \mod N$

Or, more generally: $g^x = r \mod N$, and $g^{x+p} = r \mod N$

In other words, the $p$ we’re looking for has a repeating property. If we add it to a random guess for the exponent, we get another multiple of $N$ but the remainder $r$ always stays the same.

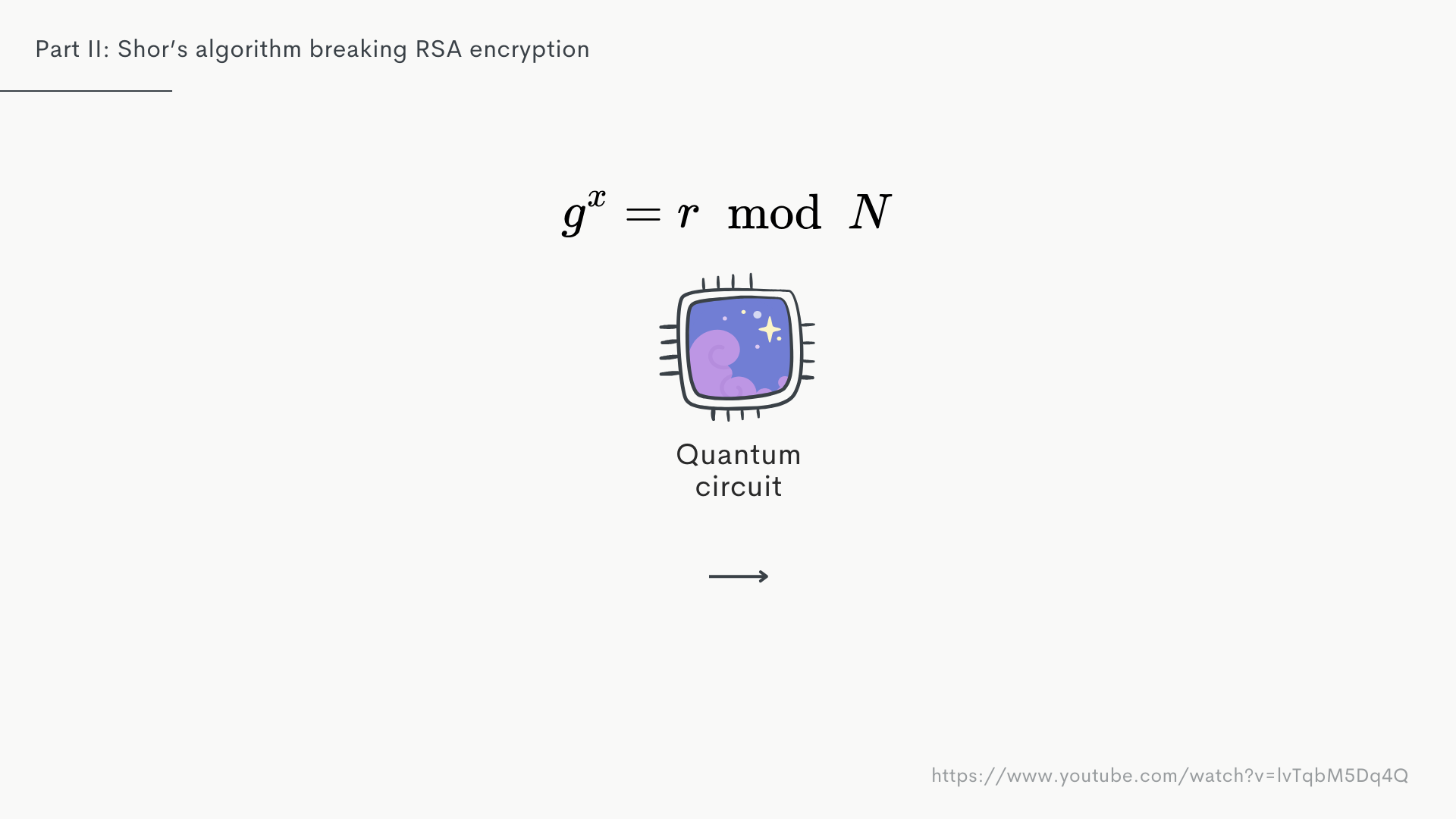
How does this help us using quantum computing?

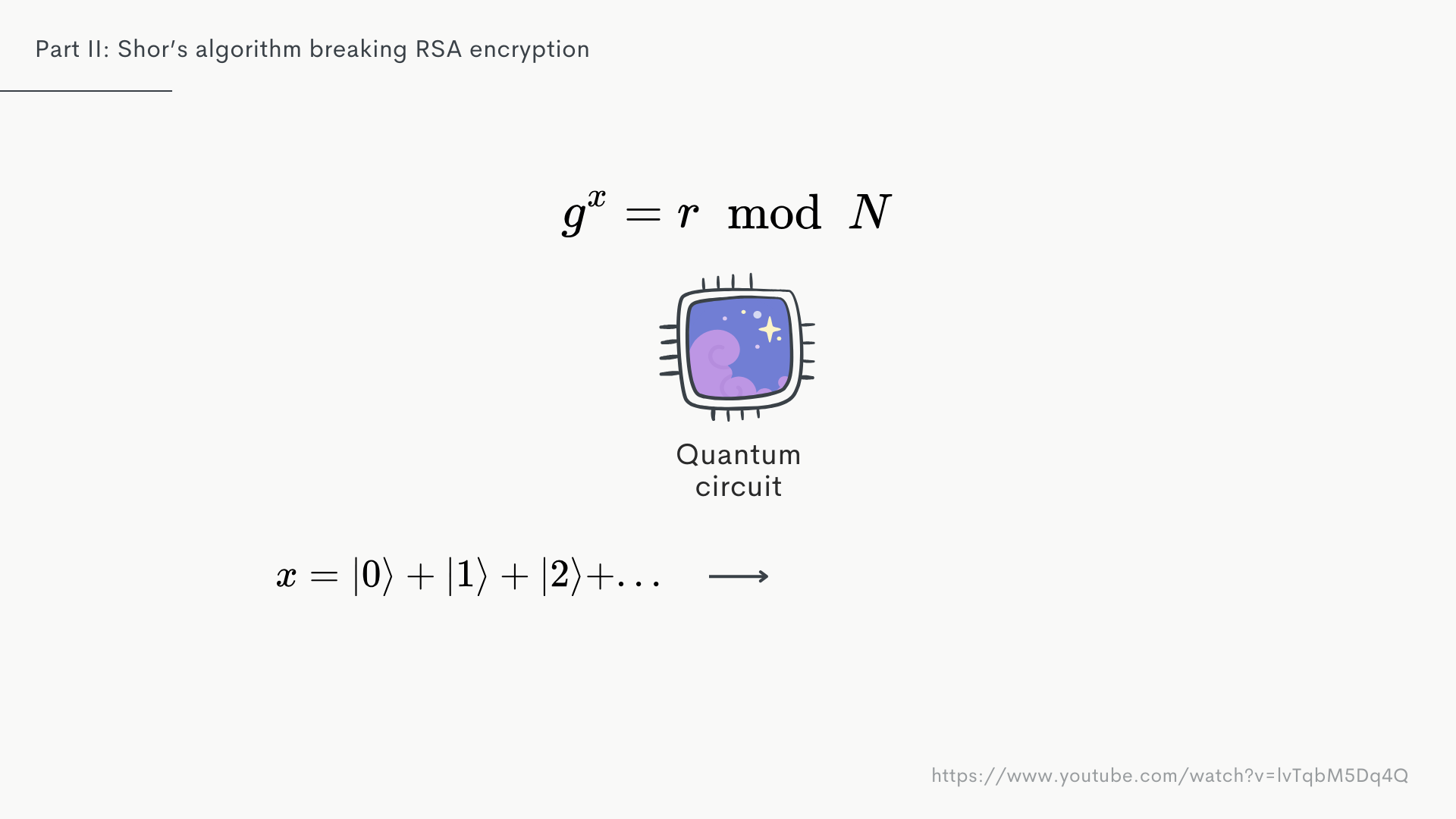
It turns our repeating properties are great for quantum algorithms, so let's have a look why.

Using a QPU, we can pass in a superposition of guesses instead of having to calculate them individually.

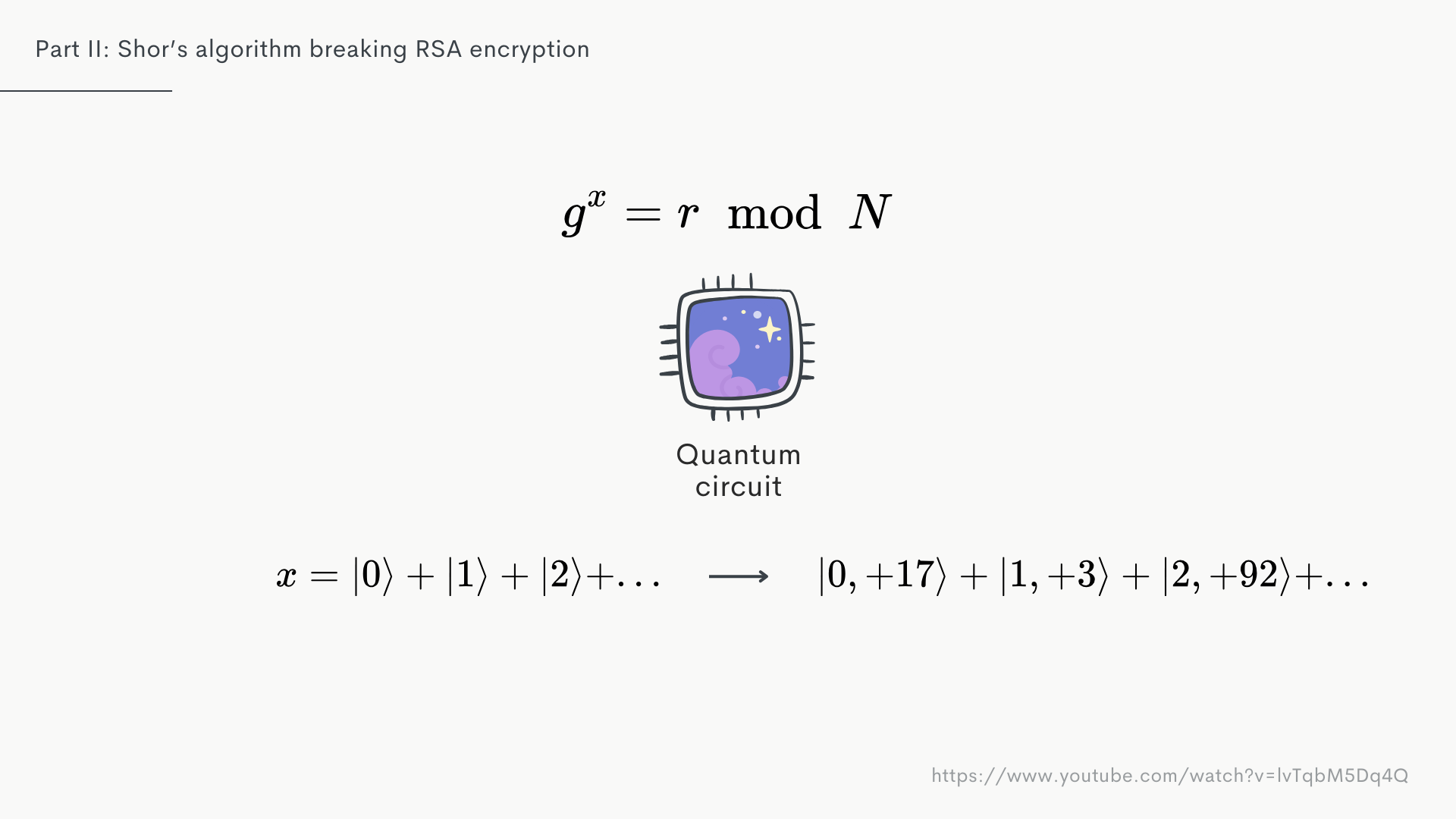
We also want to keep track of the remainder, so what we get out is a superposition of our inputs and the correlated remainders.

Now, we can’t just measure this. As we established in the beginning, this would just collapse the superposition and randomly give us one of the possible states, which is no better than us brute forcing the answer with a classical computer.

Instead, if we just measure for $r$ (and I am oversimplifying a tad here) ...

... we will get back a superposition of all the inputs that lead to whatever remainder we measured. This $r$, like we said before, is very likely not 1. But it doesn’t need to be. W really care more about the inputs themselves that led to that same remainder.

Basically, we're ending up with a superposition of inputs that we know have the repeating property of all being $p$ apart.

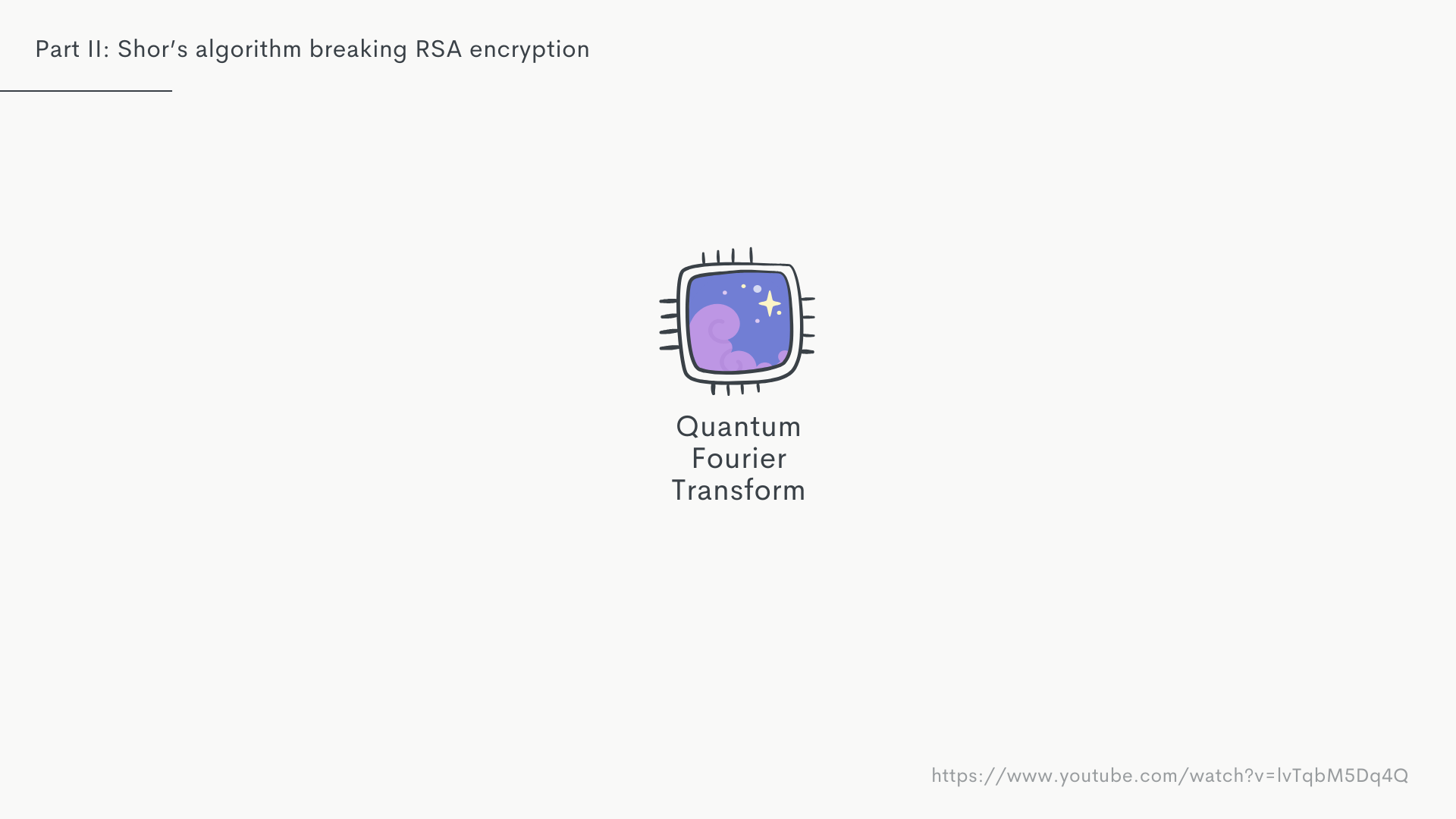
Now, there's another magical bit worth introducing here. In mathematics, when dealing with frequencies there's something called "Fourier Transforms", which generally speaking take a given frequency and breaks it up into indivudual "sinusoidal" waves that make up that frequency.

In the quantum world, we have Quantum Forier Transforms, or QFTs. A QFT takes in a superposition of numbers of a specific frequency ...

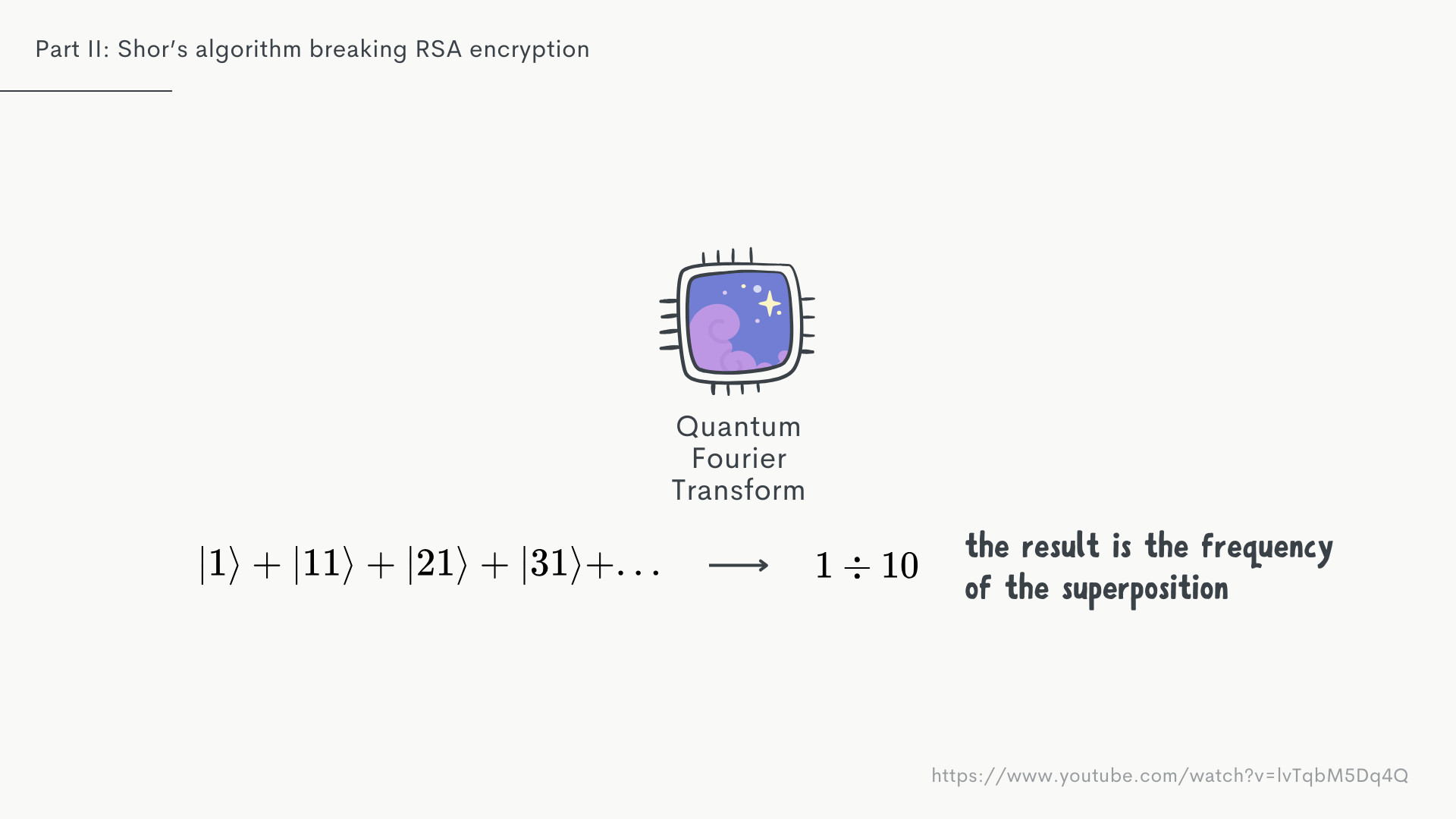
... andthrough the power of interference we get that frequency back. In our case $\frac 1 p$. Which we can easily invert to get $p$, slot it into our equoation for the better guesses and check those against the two potential problems I mentioned earlier.

In 37.5% of the time these won't occur and we have successfully broken the encryption. Tada 🎉😅

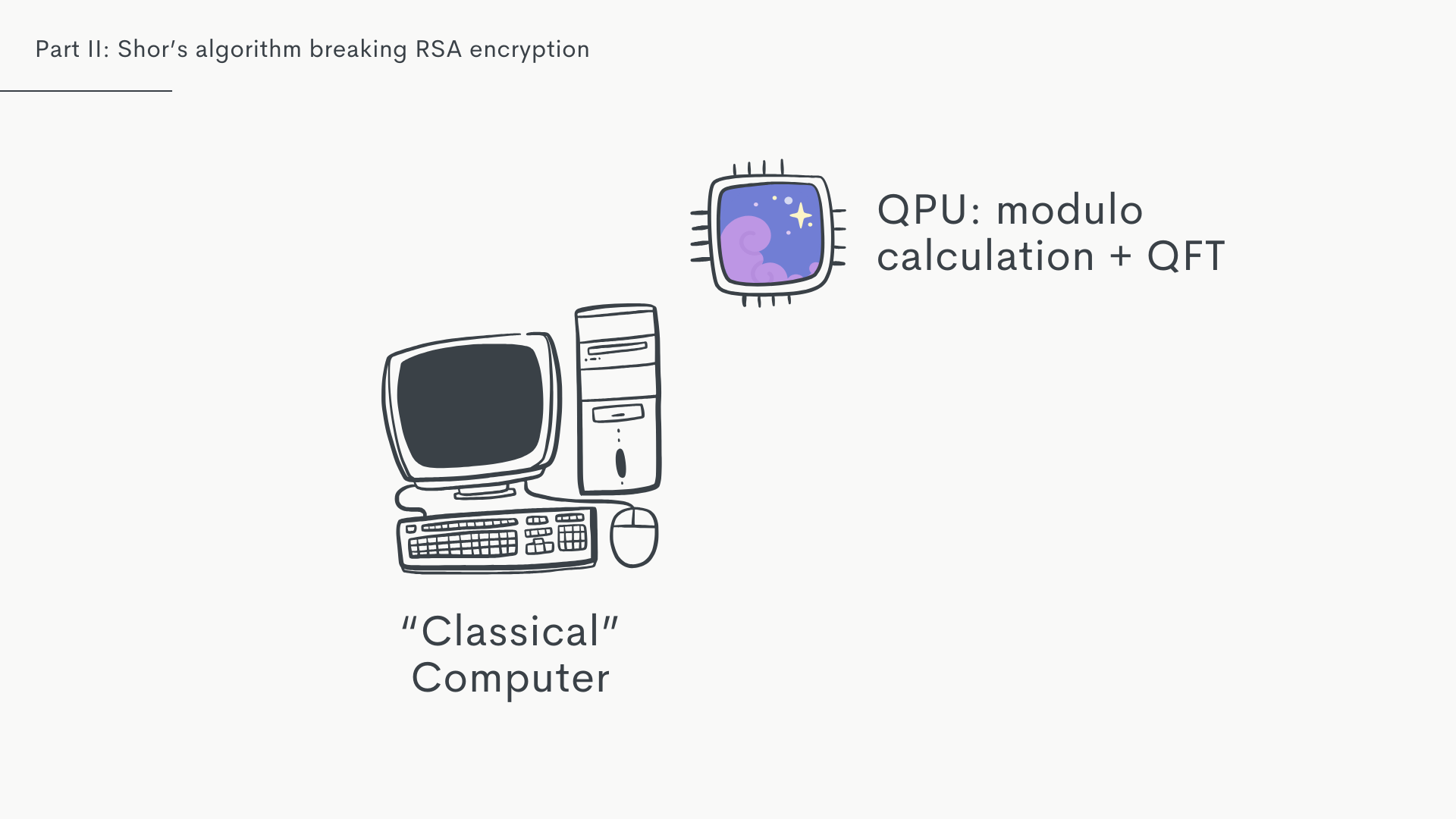
I hope this at least somewhat demonstrates that the only bit relying on the QPU and quantum computation is where we feed a superposition of our guesses for $p$ into the quantum circuit, to then find $p$ using a QFT. Everything else is just standard maths that can be done on a normal classical computer.

This is how I imagine the future of software engineering will be, once QPUs become more widely available. Realistically as a "classical" dev you don't even need to know how the quantum algorithms work exactly. You just need to know what they do - as in, what problem they solve - and there'll likely be an easy interface to access them on demand, be it through an actual QPU on your machine, or (more likely), some QPU available through the cloud.

For what it’s worth, there is no need to get worried just yet. We need a lot more qubits than the early quantum computers built by the likes of Google, IBM and other currently have to store enough memory to be able to run Shor’s algorithm on large numbers. But I do believe that inevitably we will eventually get there, so it’s good to be aware of the thread.

So are a lot of smart people, that are already working on post-quantum encryption methods to replace RSA. Which we want to switch to as soon as possible, to prevent what is called "harvest-now, decrypt-later" attacks, where the attackers just store the encrypted information they stole to then some time in the future decrypt it once the technology to do so is available. You can see why big financial backers like banks and online providers have a huge incentive to help prevent that.

Google in particular has been pretty vocal in this field and announced at the end of 2022 that they started using post-quantum-cryptography internally. They are also driving the progress together with other companies and researchers towards a standardisation for this.

Many of the most promising candidates, like kyber e.g., are lattice based. I'm not going to go into detail here, but it's essentially a vector based math problem that's really hard to solve in higher dimensions, even for with quantum algorithms.

But it does lead us to the more general question: why don’t we have functioning QPUs today.

As I said, one of the reasons is just the number of qubits and therefore currently memory limits, which keep increasing as time goes on. I’m not sure how accurate it is, but based on a list of current QPUs the top end currenty seems to lie at around 1024 qubits, which actually sounds like a lot. For comparision though, it’s estimated that to run Shor’s algorithm efficiently you would need around 2 million qubits.

However, another big problem is error correction. Maintaining the superpositions in your quantum state can be extremely challenging, since, like we’ve seen, any form of outside influence can lead to the state collapsing.

This actually seems to be the core challenge at the moment is finding ways to efficiently build error correction into the system to deal with that. It also means those qubit numbers I just mentioned should be treated with a grain of salt; often you see numbers reported as “physical qubits”, which is the number of qubits the system has, and “effective qubits”, which is the number of qubits that can be used for computation and leaves out the ones used for error correction, so “effective qubits” is a much more accurate representation of potential memory limits.

This seems to have lead to a situation where some manufacturers don't seem to focus on the error correction part too much, leading to computers that are often described as “noisy”, which refers to noise as part of the potentially erronious qubits. Again, like I said, I'm not actually working in the quantum computing field myself, so treat all of this with a grain of salt.

In any way, let’s put our head of excitement back on and assume for a moment those challenges can and will be overcome. What are some of the other uses cases for QPUs? This is a fair question, since one of the big criticisms of QPUs is that they are very interesting but are lacking practical applications. So let’s take a look at that.

The first one is kind of jumping onto the current AI and ML hype train: a whole field called quantum machine learning (QML).

It focuses on the benefits of quantum computation in the machine learning context. While it’s mostly coming down to speed, accuracy and ability to deal with more complex (e.g. higher dimensional) data sets through the use of superpositions and quantum algorithms for the various application (e.g. training models), it also seems to come down on a few core QPU uses to achieve that, so I thought they’d be worth mentioning here.

One is Quantum Fourier Transforms, which we've just seen an example of. In general being able to utilise them dealing with frequencies and repeating patterns can be extremely powerful.

Another one is Grover’s algorithm, one of the very early algorithms developed I believe. It deals with databases and provides a more efficient method for dealing with unstructured data sets. So it’s not very applicable to modern databases per se, like your usual SQL or Postgres ones, since those are mostly structured. But we can still find applications for it in other fields, e.g. in machine learning.

And lastly there's Quantum Annealing. Like with regular annealing, the goal is to find a local minimum as quickly as possible. Quantum annealing takes advantage of a phenomenon called quantum tunnelling.

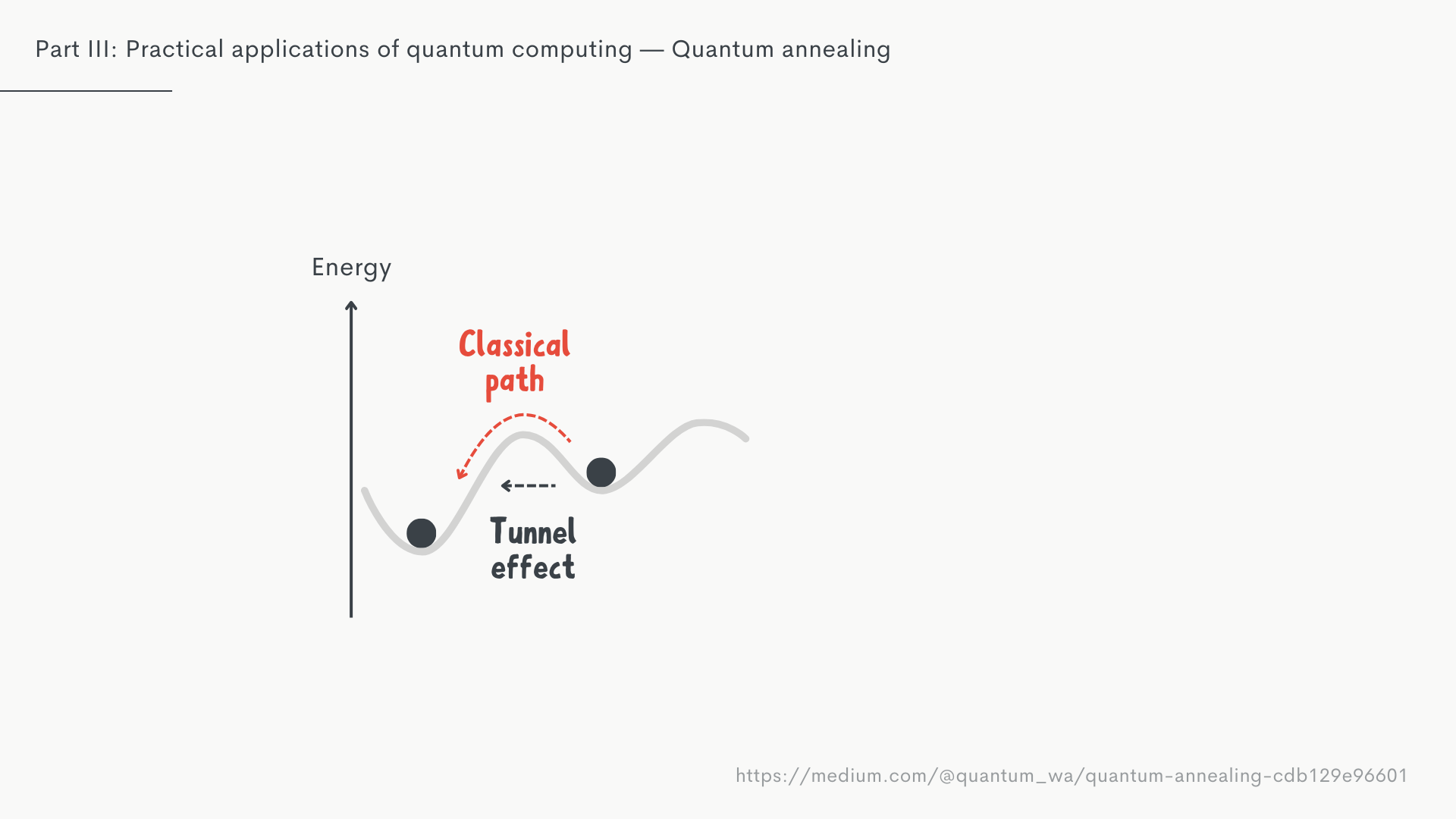
In very basic terms, quantum tunnelling describes the ability for particles to have a probability to pass through small barriers to get a lower energy state, instead of having to go over higher energy states to get to the "valley".

Unrelated to all of this, but this is another topic that’s great for wasting weekends on: quantum tunneling and what implications that theoretically can have on physics and the world as we know it; if you’re interested and don’t mind more dooms day scenarios, google “vacuum decay” 💀

Again, these can all be used to speed up machine learning computation, e.g. training models, classifications and inference and to allow us to deal with larger and more complex data sets. E.g. through “quantum principle component analysis”, which promises better performance and accuracy compared to classical methods when transforming a large dataset into a smaller one that still contains most of the original information.

At the end of the day, faster processing and larger, more complex data sets promise to lead to better and more accurate models, leading to improvements of applications of those models.

For very similar reasons, quantum computing can be really useful to speed up simulations.

QPUs provide a huge potential for improving a category of what we call optimisation problems. A pretty famous bench mark for that is the travelling salesman problem.

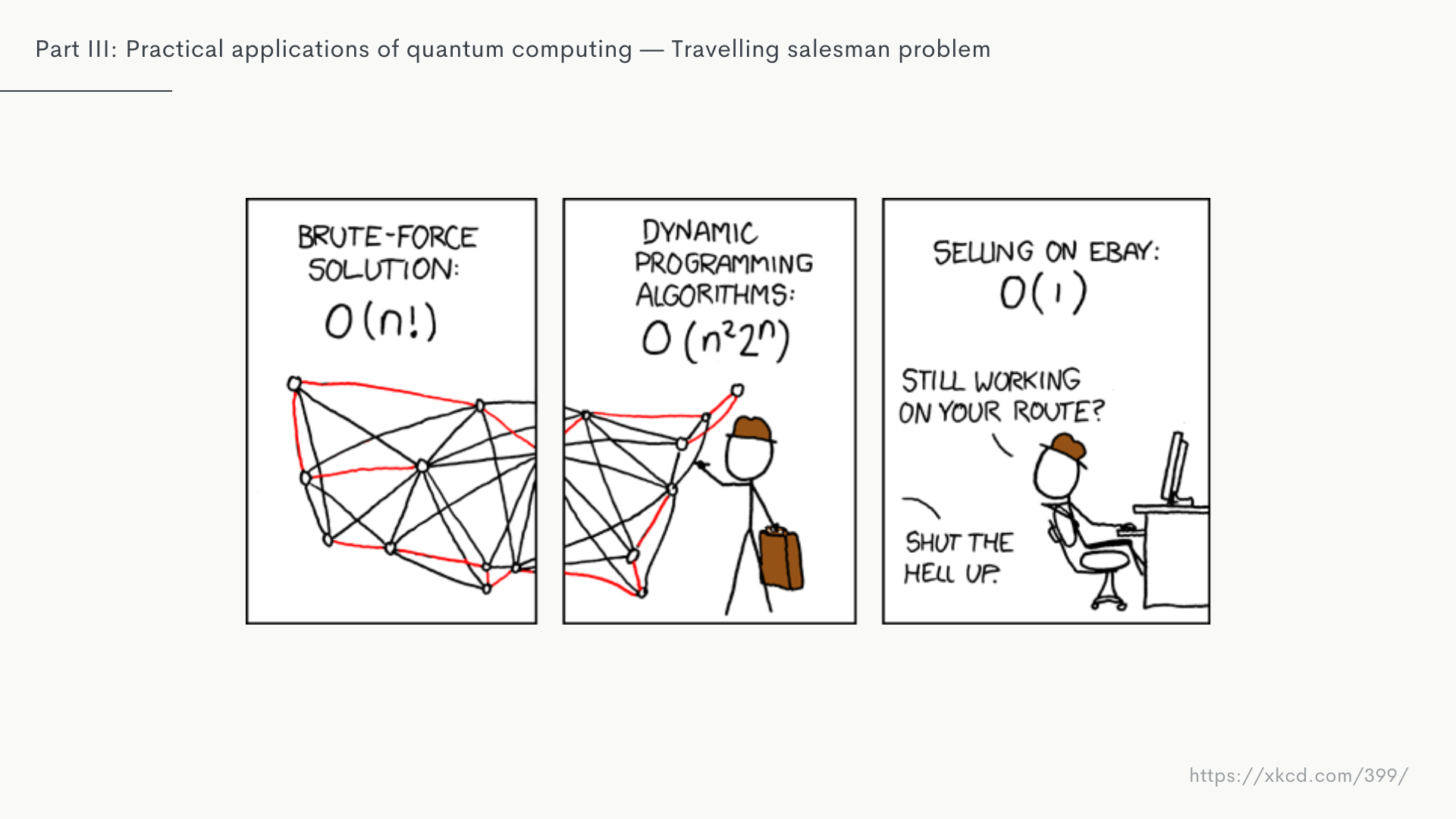
It’s essentially a thought experiment where a salesman has to visit a certain number of cities, before returning home. The challenge is to calculate the most efficient route, aka the route with the least amount of distance travelled, to achieve the goal.

For a small number of cities this is still fairly manageable, but it turns out for very large numbers of cities this starts to become impossible to accurately calculate with classical methods.

Improvements in this field could lead to leaps in fields like ...

Supply chain management

Financial modelling and portfolio optimisations

Traffic and fleet management optimisations. If you happen to own a lot of ships or airplanes, you'd probably be interested to find more efficient ways to use them.

Again, it's easy to see how these use cases are very appealing to large cooperations and others with big funding potential.

On top of the computational benefits that we already mentioned in the QML application, quantum computing has huge theoretical potential to help with real-word simulations, especially of quantum systems.

Feynman famously said: “Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical.”. Again, it’s the internet, so he probably didn’t say that, but I think the idea feels intuitive.

This is a picture of an analog computer. They used to be more common before digital computers took of.

More specifically: it’s a picture of what was called a “differential analyser analog computer”, which was used to predict tides for hundreds of years, including during WW2. It uses mechanical instruments to calculate tides based on a few astronomical frequencies influencing them, including the moon, the sun and the eccentricity of the lunar orbit.

Without going into too much detail here, the core idea was to build a machine that can be configured to take in these frequencies and return a frequency wave that represents the predictions for the tides over time. The benefits of analog computers are that they can take much more relevant inputs and outputs as physical representations which much wider ranges, rather than being restricted to our digital binary input and output system, so analog computers that use frequencies for inputs and outputs can be a lot more accurate dealing with frequency related problems.

Ironically, they are also more deceptable to errors. While on a classical computer, if you feed in a 0.2 instead of a 0, we can still fairly safely assume you meant 0, so the binary input automatically error corrects. Anaolg inputs are not corrected by default, so the more inputs you have and the more "calculations" you do on them, the more likely they are to accumulate slight errors that might add up to huge errors in the end.

Anyway, QPUs are not analog computers, but personally I like the analogy hoe analog stuff is better at simulating analog stuff, just like quantum stuff is better at simulating quantum stuff.

Some potential practical applications include ...

Weather simulations and forecasting, which is pretty famous to be unpredictable based on the amount of factors influencing it (and it's quantum nature to begin with).

Drug manufacturing and protein folding, which again we're making breakthroughs today, but are still limited by the amount of complexity we can deal with using our "classical" methods.

Alright, this is all I really have time for to go through today.

To recap, I hope I've been able to somewhat show how quantum computing is different to "classical" computing, how it might be applied for specific kinds of problems, and through the example of the deep dive into Shor's algorithm how QPUs will likely just sit on top of our normal computers to be accessed on demand.

Now, mainly because I mentioned it in my talk description, if you do want to explore quantum computing itself more, I want to share some resources how you can do so today.

First: Qiskit. It's IBMs development kit for quantum computing using Python. I want to be clear, I'm not sponsored or anything, there are other alternatives out there, Qiskit is just my personal choice cause it was one of the first more mature ones out there a few years back, and still feels like one of the most mature today.

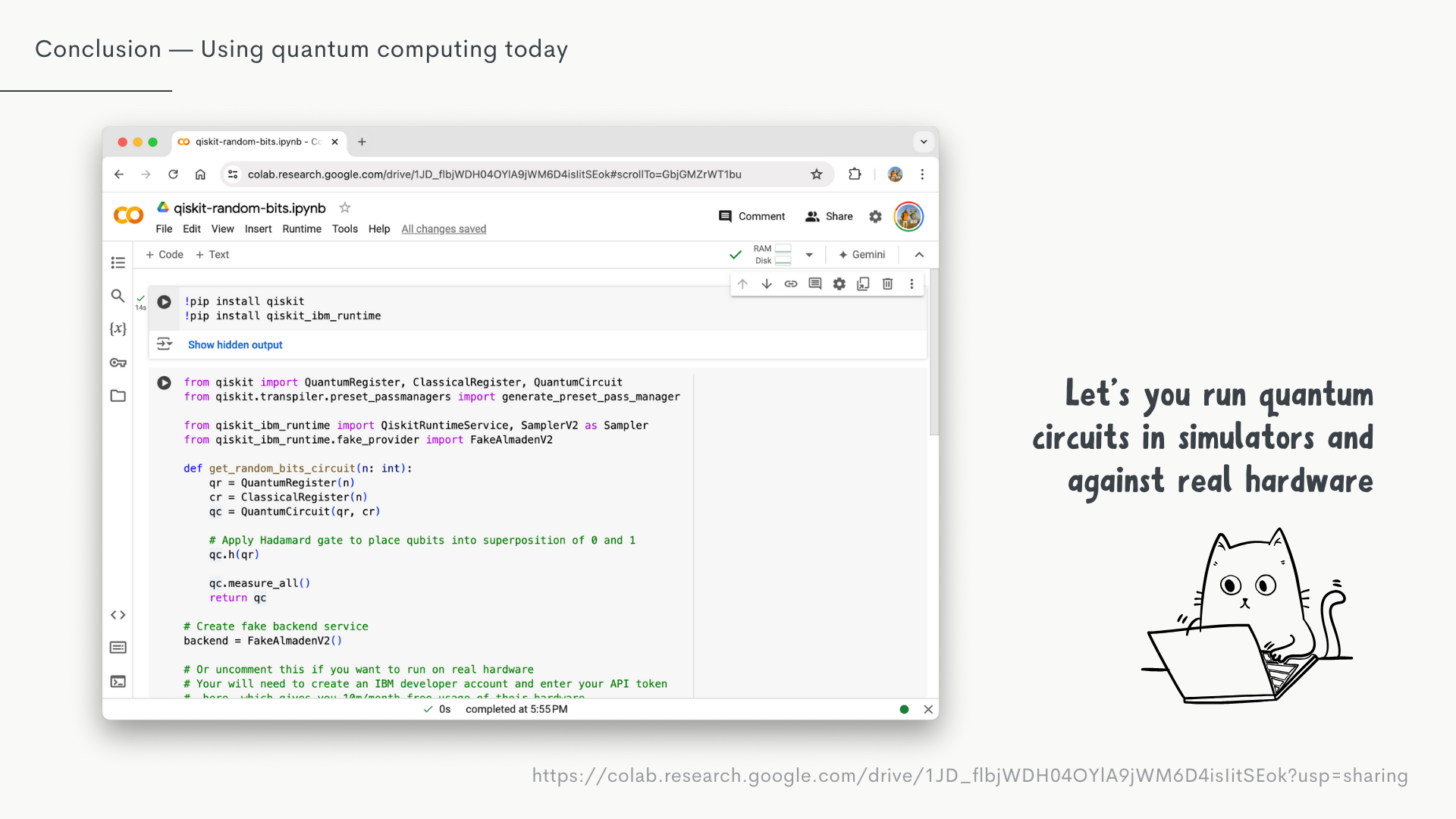
It essentially allows you to use their SDK to run quantum circuits, either on simulators, which run on your machine and are free. Or on they're actual hardware, which will cost like any other service you find online these days. But if you sign up for an IBM developer account you get 10 minutes of computation on real QPU hardware per month for free, which is pretty cool.

Like I said, it's a Python SDK, so you can set everything up to run locally, or (what I usually prefer since I don't write Python in my day-to-day) use Google Colab to run it in the cloud.

What you see here is a very simple quantum circuit I threw together yesterday, that utilises the quantum nature of qubits to return a truly random value, not like our classical counterparts that are never truly random due to the deterministic nature of classical digital computers.

Anyway, here are a few other resources I'd recommend if you want to get more into the matter; there are obviously heaps more out there, and I highly encourage you to find your own way through that forest of information, these were just some of the highlights for me personally:

Programming Quantum Computers from O'Reilly is one of the best books about the topic that really stood out to me. It's doing a great job in explain things in a simple form, while giving extremely practical applications to experiment with.

Map of quantum computing on Youtube (Channel: Domain of Science) by Dominic Walliman, who worked on actual QPUs and shares a lot of valuable insights from this space.

And more generally - again, I'm not sponsored - but besides the Qiskit specific channel IBM also maintains another Youtube channel called IBM Technology, which goes through general concepts as well as specific algorithms and applications in more depth.

And lastly, more general advice than specially for this topic: always look for free online courses from universities. Cambridge and Oxford are pretty famous for putting free courses out there every now and then, and so do other big names from all over the world.

I would recommend using books, Youtube and other lighter material first to see if this interests you at all, but once you've confirmed that, these courses are an amazing resource to really deep dive into things.